Sum to Infinity Geometric Progression

By Kur_316Britney 17 Sep, 2022 Post a Comment

Q1 Find the sum to infinity of the Geometric Progression 5 4 5 16 5 64 5 256. If a series does not have a limit or the limit is infinity then the series diverges.

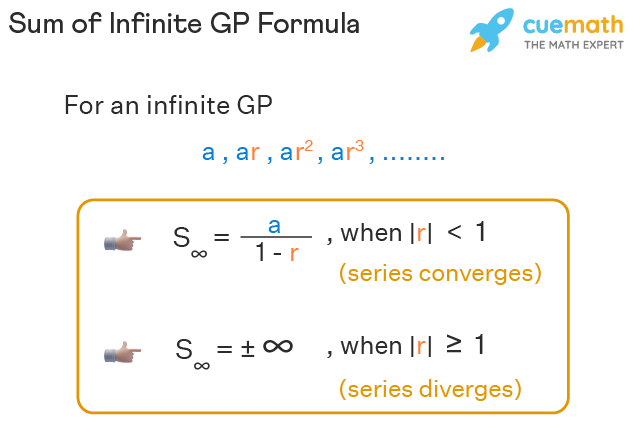
Sum Of Infinite Gp Formula Sum Of Infinite Terms Of Gp

Enter the first term and common ratio in the respective input field.

. Explains how to find the sum of an infinite geometric sequence including how to use the formula as well as when and why it is valid_____. The number of terms in infinite geometric progression will approach to infinity n. Feel free to w.

The sum of an infinite Geometric Progression with first term a and common ratio r -1 r 1 ie r 1 is S a1 - r Sum of an infinite Geometric Progression. Please try your approach on IDE first before moving on to the solution. The sum ot infinity of a geometric progression is four times the first term find the common ratio Answer by ramkikk66644 Show Source.

The sum to infinity is. This example uses simultaneous equationsDo you need more videos. In this video I will show you a simple example on how to calculate the sum to infinity of geometric progressions by appling the formula.

Tutorial on Geometric series. This is called the sum to infinity. Solved examples to find the.

Now click the button Calculate to. The infinite sum of an infinite geometric series formula is often infinity either positive or negative infinity. It is given that a_0 frac 11-r 32 and a_0 frac 1-r51-r 31 Multiplying both sides of each equation by frac 1-r1-r.

Derivation of the formula to find the sum of an infinite Geometrical Progression where common ratio is an proper fractionFor more videos on this topic visi. A 1 R -025. You can put this solution on.

Asymptote Limit of the tangent line at a point that tends. Solved Example on Sum of Infinite GP. We get a_0 32 - 32r for the first which we can.

I know that the geometric distribution follows the rules of a geometric progression thus by using the sum to infinity formula which I know its proof and is really convinced by it a 1 r. The given problem can be solved based. The sum to infinity of a geometric series is given by the formula Sa1 1-r where a1 is the first term in the series and r is found by dividing any term by the term immediately before it.

If rgeometric progression then we can sum up an infinite number of terms and still end with a finite answer. In mathematics a geometric series is the sum of an infinite number of terms that have a constant ratio between successive terms. In this lesson we will go over how to determine the sum to infintiy of a geometric series.

A geometric sequence is a sequence with a constant ratio between. Only when a certain condition is met will the infinite sum result in a. This is called the geometric progression formula of sum to infinity.

The sum in geometric progression also called geometric series is given by. The list of formulas related to GP is given below which will help in solving different. Answer 1 of 2.

The procedure to use the infinite geometric series calculator is as follows. A1 The given Geometric Progression is 5.

Proof Of The Geometric Series Formula Finite Infinite Youtube